
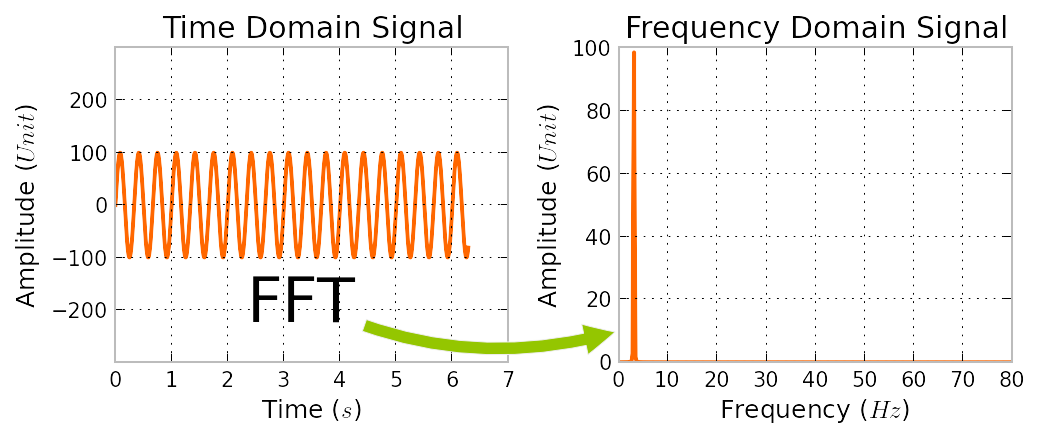
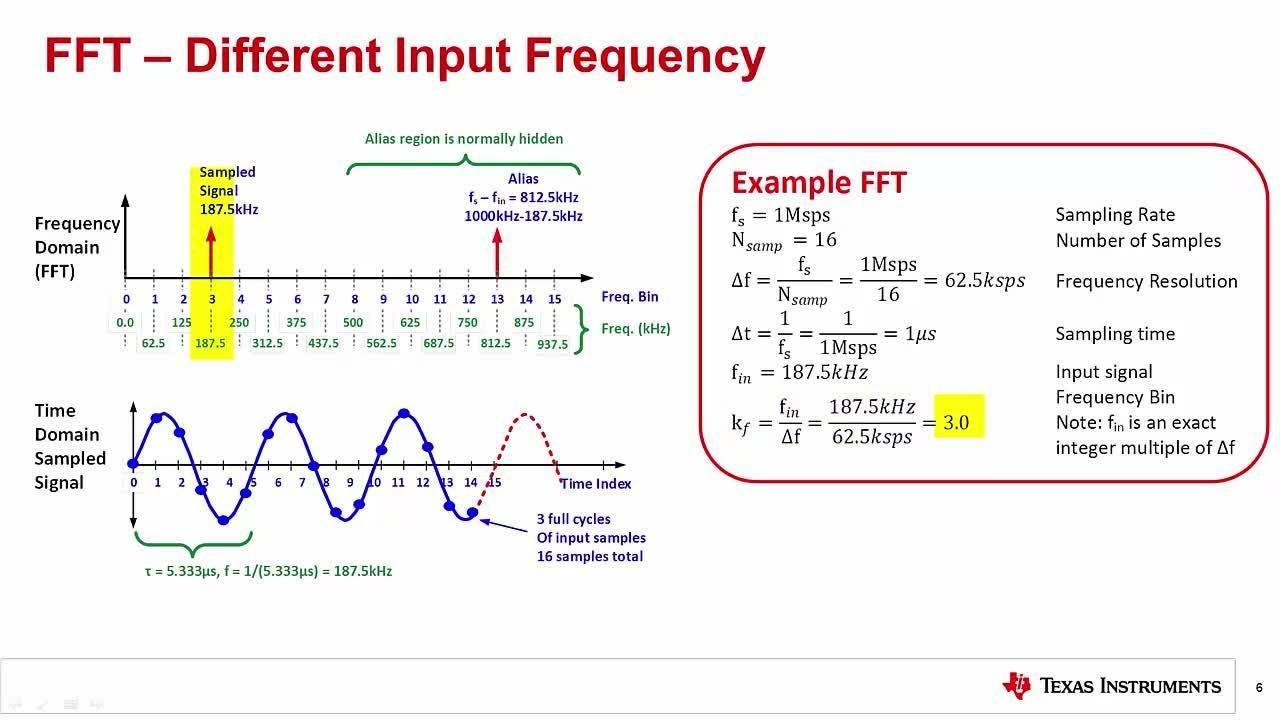
( defun fft ( a &key ( inverse nil ) &aux ( n ( length a ))) "Perform the FFT recursively on input vector A. N / 2 - 1 loop declare T : constant Complex := Odd ( Odd ' First + K ) / F ** K begin Odd ( Odd ' First + K ) := Even ( Even ' First + K ) - T Even ( Even ' First + K ) := Even ( Even ' First + K ) + T end end loop return Even & Odd end end if end FFT begin return FFT ( X, X ' Length, 1 ) end Generic_FFT = &60 A DIM Complex X ' Last ), N / 2, 2 * S ) begin for K in 0. Real ( N / 2 )) Even : Complex_Vector := FFT ( X, N / 2, 2 * S ) Odd : Complex_Vector := FFT ( X ( X ' First + S. 1 => X ( X ' First )) else declare F : constant Complex := exp ( Pi * j / Real_Arrays. As the Convolution Theorem 18 states, convolution between two functions in the spatial domain corresponds to point-wise multiplication of the two functions in the frequency domain. With Ada.Numerics with _Complex_Elementary_Functions function Generic_FFT ( X : Complex_Vector ) return Complex_Vector is package Complex_Elementary_Functions is new _Complex_Elementary_Functions (Complex_Arrays.Complex_Types ) use Ada.Numerics use Complex_Elementary_Functions use Complex_Arrays.Complex_Types function FFT ( X : Complex_Vector N, S : Positive ) return Complex_Vector is begin if N = 1 then return ( 1. The fast Fourier transform (FFT), which is detailed in next section, is a fast algorithm to calculate the DFT, but the DSFT is useful in convolution and image processing as well.


 0 kommentar(er)
0 kommentar(er)
